suscripción
El Neutrino
El neutrino es una partícula esquiva, en apariencia insignificante, pero necesaria para explicar el mundo. Ni la radiactividad, ni el big bang, ni el Modelo Estandar de la física de partículas serían posibles sin él. Con El neutrino, un blog nacido en febrero de 2009, el físico y escritor Germán Fernández pretende acercar al lector, y ahora al oyente, al mundo de la ciencia a partir de cualquier pretexto, desde un paseo por el campo o una escena de una película, hasta una noticia o el aniversario de un investigador hace tiempo olvidado.
Ménage à trois sideral: los puntos de Lagrange
Cuando pensamos en órbitas, imaginamos un cuerpo celeste describiendo un círculo o una elipse alrededor de otro. Ésta es la situación más simple, pero no es la única posible, ni mucho menos. Afortunadamente, en nuestro Sistema Solar los planetas están muy separados entre sí, y sus masas son muchísimo menores que la del Sol; por eso se mueven en órbitas elípticas alrededor de éste, y las perturbaciones que ejercen unos sobre otros son muy pequeñas. Y digo afortunadamente porque de esta manera las órbitas son muy estables. A efectos prácticos, se puede calcular el movimiento de cada planeta con bastante precisión considerando únicamente la atracción gravitatoria del Sol. Este problema es resoluble, y sus soluciones son las sencillas órbitas elípticas.
Pero en general, cuando hay más de dos cuerpos involucrados, el problema no se puede resolver analíticamente, y hay que recurrir a aproximaciones o a cálculos numéricos. Ni siquiera el llamado problema de los tres cuerpos, el que plantea el estudio del movimiento de tres cuerpos de cualquier masa sometidos a su atracción gravitatoria mutua, tiene una solución general que pueda expresarse con fórmulas matemáticas. Sí que la tiene un caso particular del problema de los tres cuerpos, el llamado problema de los tres cuerpos restringido circular, en el que se postula que la masa de uno de los cuerpos es despreciable respecto a la de los otros dos, y que éstos últimos tienen órbitas circulares: éste es el ca¬so, por ejemplo, del sistema formado por la Tierra y la Luna y una nave espacial que se mueve entre ellas.
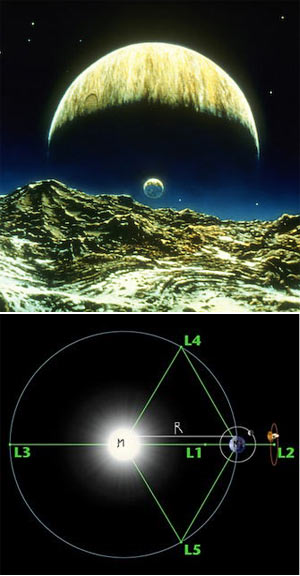
El problema de los tres cuerpos restringido circular tiene cinco soluciones estacionarias, cinco puntos en los que un objeto pequeño permanece en equilibrio estacionario respecto de los otros dos; son los llamados puntos de Lagrange o puntos de libración. El objeto, visto desde los dos cuerpos grandes, parece inmóvil en el cielo. Estos puntos de Lagrange se identifican con la letra L seguida de un número, desde 1 hasta 5.
Nuestros programas
- Hablando con Científicos
- Vanguardia de la Ciencia
- Ulises y la Ciencia
- Ciencia y genios
- Ciencia Nuestra de cada Día
- Zoo de fósiles
- Seis patas tiene la vida
- Océanos de Ciencia
- Quilo de Ciencia
- Ciencia EXtrema
- El Neutrino
- Cierta Ciencia
- Ciencia Fresca
Podcasts
Ciencia con Humor
Recomendamos
- El Neutrino
- Blog de divulgación científica de Jorge Laborda
- Cierta Ciencia
- La Aldea Irreductible
- GeoCastAway. El Podcast de Geología y Ciencias de la Tierra
- Universo Paralelo
- La Buhardilla 2.0
- Aragosaurus
- Web de aficionados a los fósiles
- El podcast del microbio
- Hablando de Ciencia
- Folklore de los Fósiles Ibéricos
- Glosopetrae
- Astrosigma
- Podcast Coffee Break
- El Pintor de las Sombras
- AstroAfición
- Blog de Laboratorio
- Locuciencia
- Noticias de la Ciencia y la Tecnología
Apoya a CienciaEs haciéndote MECENAS con una donación periódica o puntual.
36,4 millones de audios servidos desde 2009
Agradecemos la donación de:
Alejandro Acosta Espinoza
Mecenas
Jairo Ospino Rodriguez
Mecenas
Rafa Castillejo
“Soy profesor de física y química en un instituto de enseñanza secundaria en Mijas Costa y este año he utilizado los podcasts de CienciaEs para que los alumnos hicieran exposiciones a sus compañeros sobre los temas que ellos elegían.”
Mecenas
Javier Gorriz Ortiz
Mecenas
Fidel Díaz Rodríguez
Mecenas
Anónimo
“Miles de gracias por el esfuerzo y felicitaciones a todos, en particular a la Dra Josefina Cano por sus doscientas aportaciones. Acepten un abrazo agradecido desde México.”
Mecenas
Carlos Serrano
Mecenas
Eulogio González Moreno
“Encantado de apoyaros. Realizáis unos programas estupendos.”
Mecenas
Wendy Trollope
Mecenas
Angel Manuel García Martín
Mecenas
Mauro Mas
Mecenas a través de Patreon
María Elena García Martín
Mecenas a través de Patreon
Anónimo
“Agradecido por su esfuerzo, los saludo desde México.”
Mecenas
Pilar Soler
Mecenas
Francisco Javier Gallegos Casado
Mecenas
Daniel Faba Corral
Mecenas
Marcos López Montes
Mecenas
José Luis Moreno González
Mecenas
Alvaro Vallejo
“Muchísimas gracias por tan maravilloso trabajo de divulgación. Ustedes me acompañan varias horas al día, todos los días.”
Mecenas
Juan Gomez-Cuetara
“¡Una gran programa!!! Es de agradecer que deis difusión a lo que los científicos españoles están haciendo.”
Mecenas
Alfredo Diaz Miranda
“Mi profundo y sincero agradecimiento para todos en CienciaEs pero en especial para Angel Lozano y Jorge Laborda por la esmerada labor que realizan.”
Mecenas
Jorge Valencia Jiménez
Mecenas
Anónimo
“Tarde pero sin sueño, mis admirados divulgadores. Un abrazo agradecido desde el otro lado del Atlántico.”
Mecenas
María del Carmen Colodrero
Joaquín Méndez Colodrero
Mecenas
Carlos Fernández
Mecenas
Carlos Garcia Gutiérrez
Mecenas
Marian y Miguel Ángel
“Muchas gracias por tu trabajo. La Ciencia al alcance de todos.”
Mecenas
Carlos Serrano
“Un placer cooperar un poco con su proyecto. Buen trabajo!”
Mecenas
Francisco Javier Aguilar
Mecenas
Francisco J. García Pato
Mecenas
Jesús López Tapia
“Querido Ángel. Me siento muy honrado de pertenecer a esta comunidad. Gracias por vuestro trabajo.”
Mecenas
Javier Olveira
“Gracias por seguir realizando divulgación de calidad.”
Mecenas
Sara Carrero
“Aprovecho para daros la enhorabuena por el espacio “Hablando con Científicos”, que me gusta especialmente.”
Mecenas
Mariano Redondo de la Villa
Mecenas
Javi Zumaia
“En plena era de la desinformación, vuestra labor dedicada a la divulgación científica no hace sino aportar un balón de oxígeno a todos los amantes de la ciencia.”
Mecenas
———- O ———-
———- O ———-
Suscribase a nuestros programas
