El Sol, y la energía que de él nos llega, y la Tierra, con su rotación, mantienen los océanos y la atmósfera en continuo movimiento.

En la primera parte de este programa les contamos cómo la diferencia de temperaturas entre el Ecuador y los Polos, generada por la radiación que nos llega del Sol, es capaz de poner en marcha corrientes de aire (vientos) y agua (corrientes marinas). Es, por tanto, la radiación solar el factor principal que mantiene las corrientes marinas.

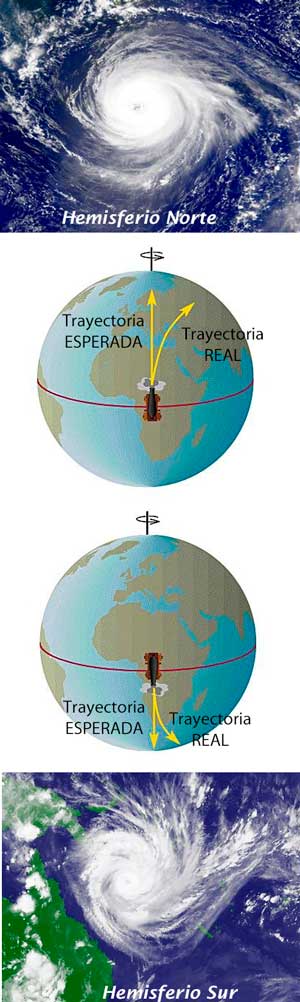
En esta segunda parte les hablamos del otro factor: la rotación terrestre. La rotación de la Tierra en torno al eje Norte-Sur que conecta sus Polos, juega un papel sutil pero fundamental para conocer las trayectorias de esas corrientes. El efecto principal de la rotación es curvar las trayectorias de las corrientes. Concretamente, tiende a desviarlas hacia la derecha en el sentido del movimiento en el hemisferio Norte y hacia su izquierda en el hemisferio Sur. A este curioso efecto se le denomina efecto Coriolis; nombrado así en honor al científico francés Gustave Coriolis por sus estudios de cuerpos en rotación. El efecto Coriolis no sólo hace girar las corrientes marinas, sino también las masas de aire de la atmósfera (piensen ustedes, por ejemplo, en los grandes giros o remolinos que llamamos borrascas y anticlones, y que seguramente hayan visto en algún parte del tiempo meteorológico).

Ahora la cuestión es ¿por qué vemos que giran y no vemos trayectorias rectilíneas? Sigan, por favor, el siguiente ejemplo que ustedes mismos podrán experimentar.

Puede que en su pueblo o ciudad o en su mismo barrio haya un parque infantil con un carrusel. En realidad, estos carruseles no son más que plataformas giratorias, por lo general circulares y con un eje de rotación en el centro, quizás incluso con asientos, y que al hacerlo girar suelen hacer las delicias de los pequeños y de algún que otro grande. Uno de estos carruseles nos va a servir como Tierra improvisada. Estos carruseles comparten con la Tierra el hecho de girar alrededor de un eje, y la diferencia evidente de que sea una superficie plana y no esférica la que rota no va a cambiar en exceso la comparación.

Imagine que una tarde, dos hermanos, uno de pelo rubio y otro moreno, se encuentran en el parque infantil junto con su padre, que les vigila con cierto aire distraído. Los chicos, algo aburridos, deciden montarse en el carrusel. Ambos corren e impulsan el carrusel haciéndolo girar rápidamente en sentido contrario a las agujas del reloj. Se montan a la carrera y ambos se sientan cara a cara: el chico moreno en el borde del carrusel y su hermano rubio se sienta sobre el eje de rotación. Si mantenemos la analogía con la Tierra es como si el chico rubio estuviera en el Polo Norte y el chico moreno estuviera sentado en una zona próxima al Ecuador.

Los dos chicos giran solidariamente con el carrusel sin perderse de vista y manteniéndose la distancia que los separa, pero ambos se desplazan a velocidades muy distintas. Mientras que el chico rubio, en el eje de rotación, se mueve muy poco (lo único que hace es rotar), el chico moreno, más alejado del eje de rotación, se desplaza a mayor velocidad en sentido anti-horario. Este hecho es fundamental: la velocidad disminuye cuanto más cerca estemos del eje de rotación. Lo mismo ocurre en la Tierra. Una persona que esté en el Ecuador se encuentra exactamente a un radio terrestre de distancia del eje de rotación, y se desplaza a la vertiginosa velocidad de 1620 km/h hacia el Este. En cambio, otra persona que se encuentre en el Polo Norte, está justo sobre el eje de rotación y no experimenta desplazamiento alguno (solo rota, como el chico rubio).

Pues bien, con el carrusel en movimiento, el chico sentado en el borde (el moreno) saca ahora una pelota de tenis y se la lanza, no muy fuerte, a su hermano rubio. La pelota sale de la mano del chico moreno y ambos, expectantes, la siguen con la mirada. Pero, conforme la pelota avanza en el aire y el carrusel sigue su rápido movimiento de rotación, ambos observan sorprendidos cómo la trayectoria de la pelota parece curvarse hacia la derecha del lanzador, siendo imposible para el chico rubio capturarla.

¿Qué es lo que ha ocurrido? El chico moreno, con la intención de hacerle llegar la pelota a su hermano rubio, ha tenido que impulsar la pelota con una cierta velocidad de salida en dirección al centro del carrusel. Pero como estaba sentado al borde, a esta velocidad hay que superponerle la velocidad a la que se mueve el borde del carrusel. Por tanto, cuando la pelota sale de la mano del chico moreno, tiene una velocidad de salida compuesta por la suma de ambos movimientos: uno hacia el eje de rotación donde está el chico rubio, y otro, causado por el movimiento de rotación, hacia la derecha del lanzador (recuerden que el giro del carrusel era precisamente en sentido anti-horario, hacia la derecha del lanzador). Un aspecto importante es que, una vez lanzada, la pelota ya no participa del movimiento de rotación puesto que va por el aire y, si nadie la intercepta y despreciamos el rozamiento con el aire, conserva su velocidad en ambas direcciones.

Pues bien, la pelota ya ha sido lanzada y se va alejando del borde hacia el eje del carrusel. Sin embargo, según se va acercando al eje de rotación, va encontrando por debajo un suelo que cada vez tiene una menor velocidad en el sentido de giro (recuerden que la velocidad disminuye cuanto más cerca se esté del eje de rotación). Eso significa que la velocidad de la pelota en el sentido de giro (hacia la derecha del lanzador) es mayor que la del suelo en el mismo punto. El resultado es que ambos chicos ven como la pelota se adelanta respecto del suelo. Por ejemplo, el chico moreno que lanzó la pelota desde el borde ve como la trayectoria de la pelota se curva hacia su derecha.

Es fácil imaginar que los hermanos no hubieran observado esta desviación de la trayectoria de la pelota si el carrusel fuera pequeño, o si la velocidad de rotación fuera pequeña, o si el lanzamiento hubiera sido tan rápido que no hubiera dado tiempo a que el carrusel hubiera girado un ángulo apreciable antes de que la pelota recorra la distancia desde el borde hasta el centro. Por otra parte, esta desviación de la trayectoria es una desviación aparente, percibida por los chavales por están sentados en una superficie en rotación. Otro observador fijo, no sujeto a rotación alguna, como su padre que les observaba atentamente desde fuera, no observaría tal desviación, tal giro, sino que vería que la trayectoria de la pelota es la habitual de un lanzamiento, sin giros extraños.

En el caso de la Tierra, ocurre algo similar. Observamos que las trayectorias de las corrientes de aire o de agua se curvan (1) por encontrarnos nosotros mismos sobre una superficie en rotación y (2) porque distintos puntos de la superficie se desplazan a velocidades distintas (las zonas cercanas a los Polos se mueven más lentamente que las zonas situadas cerca del Ecuador). Como estas corrientes recorren grandes distancias y, a escala planetaria, son relativamente lentos, da tiempo a que el arco barrido por la rotación terrestre sea apreciable y, por lo tanto, el giro observado en sus trayectorias también lo es. Otros cuerpos en movimiento como aviones o proyectiles que también se desplazan grandes distancias deben corregir su movimiento teniendo en cuenta la rotación terrestre.

A menor escala, en situaciones más de andar por casa, el efecto de la rotación terrestre en los cuerpos en movimiento es inapreciable. Por ejemplo, en ningún deporte un jugador tiene que tener en cuenta la rotación de la Tierra para hacerle llegar la pelota a un compañero. Algunos argumentan que los vórtices o remolinos que se forman en los sumideros de las duchas, fregaderos, lavabos, etc. son debidos a la rotación terrestre, pero esto no es cierto. Si bien el agua que se va por el desagüe se ve sometida a la fuerza de Coriolis, su efecto es miles de veces más débil que otros factores como la turbulencia, la posición del grifo, la forma de la pieza, etc.

REFERENCIAS

- “El Clima”. Manuel Toharia (2006). ISBN: 978-8-4830-6683-6.

- “Ocean Circulation”. E. Brown y otros. Open University. ISBN: 978-0-7506-5278-0

OTROS PROGRAMAS RELACIONADOS

- Océanos en movimiento (I): La radiación solar.

- Energía del viento en el mar. Hablamos con Manuel Pérez.

- ¿A qué velocidad nos movemos por el Universo?

Video sobre la aceleración de Coriolis